DFS와 BFS를 언제 써야 할까 - 그래프 탐색을 이해하는 사고의 흐름

이 문서는 그래프 탐색의 대표적인 방법인 DFS와 BFS를 단순히 어떻게 사용하는지가 아니라, 왜 이런 방식으로 동작하는지를 이해하는 데 초점을 맞춰요.
또한 문제를 마주했을 때 어떤 기준으로 탐색 방법을 선택해야 하는지까지 함께 정리해 보려고 해요.

 

이 문서를 읽고 나면 아래 질문에 스스로 답할 수 있게 될 거예요.

• 이 문제는 모든 경우를 끝까지 탐색해야 할까요?
• 최단 거리나 이동 횟수가 중요한 문제일까요?
• 이런 조건에서 DFS와 BFS 중 어떤 탐색을 선택하는 게 맞을까요?

 

왜 그래프 탐색이 중요한가요?

---

그래프 탐색은 알고리즘 문제에서 반복해서 등장하는 핵심 개념이에요.
문제의 형태는 달라 보여도, 내부를 들여다보면 정점과 간선을 따라 이동하며 답을 찾는 구조인 경우가 많아요.

 

그래프 탐색은 아래와 같은 상황에서 자연스럽게 사용돼요.

• 미로에서 출구 찾기
  현재 위치에서 이동할 수 있는 경로를 따라가며 도착 지점을 탐색해요.
• 최단 거리 계산
  두 지점 사이를 가장 적은 이동 횟수로 도달해야 하는 문제예요.
• 친구 관계 / 추천 시스템
  사람 간의 연결 관계를 따라가며 관계의 깊이나 범위를 파악해요.

이처럼 서로 다른 문제처럼 보이지만, 모두 어디까지, 어떤 순서로 탐색할 것인가라는 공통된 질문을 포함하고 있어요.

 

그래프 탐색을 이해하기 위해 가장 먼저 던져야 할 질문은 이거예요.

 

모든 경우를 빠짐없이 탐색하려면 어떻게 해야 할까?

 

이 질문에 대한 서로 다른 두 가지 답이 바로 DFS와 BFS라는 탐색 전략이에요.

 

이제부터는 이 두 방법이 어떤 기준으로 탐색 순서를 결정하는지, 그리고 어떤 문제에서 더 적합한지를 하나씩 살펴볼 거예요.

 

그래프 탐색의 기본 개념

---

그래프 탐색을 잘 이해하려면, 먼저 그래프를 문제 해결 관점에서 바라보는 게 중요해요.

그래프는 보통 두 가지 요소로 구성돼요.

• 정점(Vertex): 우리가 방문해야 할 지점이에요.
  예를 들어 미로의 각 칸, 지도 위의 도시, 사람 한 명이 될 수 있어요.
• 간선(Edge): 한 정점에서 다른 정점으로 이동할 수 있는 경로예요.

여기서는 복잡한 수학적 정의보다, 길을 따라 이동하면서 다음 지점을 방문한다는 개념으로 이해하면 충분해요.
그래프 탐색은 결국 어디로 이동할 수 있는지 확인하고, 그 길을 따라가는 과정이에요.

 

그 과정에서 반드시 등장하는 개념이 방문 처리(visited)라는 개념이에요.
그렇다면 이런 질문을 던져볼 수 있어요.

 

한 번 방문한 곳을 계속 다시 방문하면 어떤 문제가 생길까?

 

일반적인 그래프 탐색 문제에서 방문한 곳을 다시 방문한다면 아래와 같은 문제를 마주할 수 있어요.

• 무한 루프
  같은 정점을 계속 오가면서 탐색이 끝나지 않을 수 있어요.
• 불필요한 계산
  이미 확인한 경로를 다시 탐색하느라 쓸데없이 시간이 소모돼요.
• 시간 초과
  탐색 범위가 커질수록 중복 방문이 누적되어 성능 문제가 생겨요.

그래서 그래프 탐색에서는 이미 방문한 정점은 다시 방문하지 않도록 기록하는 것이 필수예요.

이 방문 처리 덕분에 탐색을 안전하고 효율적으로 진행할 수 있어요.

 

DFS (Depth-First Search) — 깊이 우선 탐색

---

DFS는 그래프 탐색에서 가장 먼저 접하게 되는 기본적인 방법이에요.
이름 그대로 한 방향으로 최대한 깊게 들어가는 방식이 핵심이에요.

 

DFS의 탐색 전략은 단순해요.

• 갈 수 있을 때까지 최대한 깊게 이동해요.
• 더 이상 갈 수 없으면 이전 지점으로 되돌아와요.

즉, 한 경로를 끝까지 탐색한 뒤에야 다른 경로를 살펴보는 방식이에요.

 

DFS의 동작 방식

DFS는 구조적으로 스택(Stack) 기반 사고와 잘 맞아요.

• 현재 위치를 기준으로 다음 위치로 이동하면서, 이전 상태를 스택에 쌓아요.
• 더 이상 이동할 수 없으면 스택에서 하나씩 꺼내며 되돌아와요.

이 때문에 DFS는 재귀 함수와 자연스럽게 연결돼요.
재귀 호출 자체가 호출 스택을 사용하기 때문에, DFS의 동작 흐름을 그대로 표현할 수 있어요.

또한 DFS의 방문 순서는 다음과 같은 특징을 가져요.

• 한 경로를 끝까지 탐색한 뒤에야 다른 경로를 방문해요.
• 탐색 순서는 그래프 구조와 인접 리스트의 순서에 크게 영향을 받아요.

코드로 한번 살펴볼까요?

void dfs(int cur) {
    visited[cur] = true;
    for (int next : graph[cur]) {
        if (!visited[next]) {
            dfs(next);
        }
    }
}

 

위 코드는 DFS를 나타내는 가장 기본적인 형태예요.

코드를 흐름대로 보면 이렇게 동작해요.

1. 현재 정점 cur를 방문 처리해요.
2. cur와 인접한 정점들을 하나씩 확인해요.
3. 아직 방문하지 않은 정점이 있다면, 그 정점으로 다시 DFS를 호출해요.
4. 더 이상 갈 수 있는 정점이 없으면, 함수가 종료되면서 이전 호출 지점으로 돌아가요.

이 재귀 호출 흐름이 바로 깊게 들어갔다가 되돌아오는 DFS의 핵심 동작이에요.

 

DFS의 특징을 정리하면 다음과 같아요.

• 구현이 직관적이에요.
  재귀를 사용하면 코드가 간결해요.
• 모든 경우를 탐색해야 하는 문제에 적합해요.
  가능한 경로를 전부 확인해야 하는 상황에서 유용해요.
• 최단 거리 문제에는 부적합한 경우가 많아요.
  가장 먼저 도착한 경로가 최단 경로라는 보장이 없어요.

 

BFS (Breadth-First Search) — 너비 우선 탐색

---

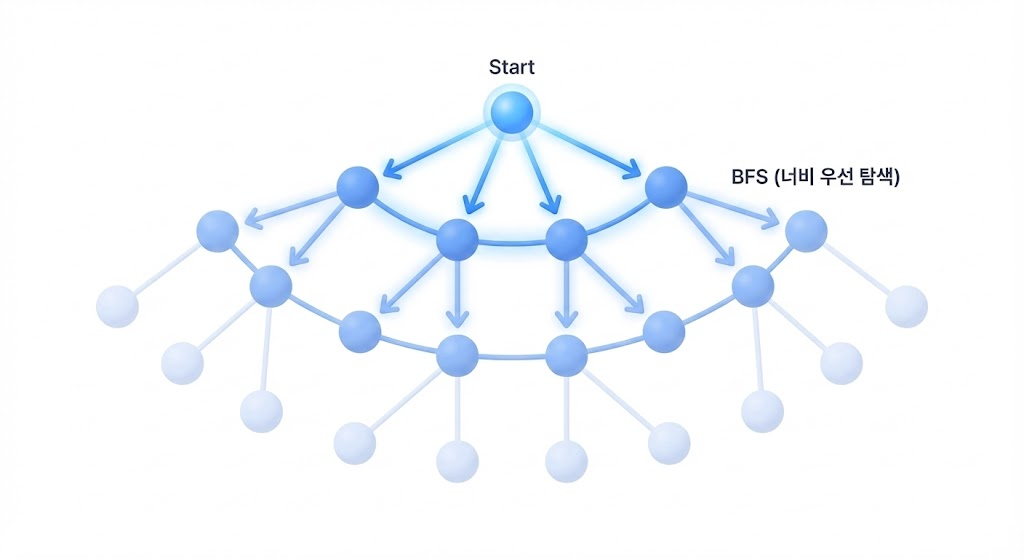
BFS는 DFS와 달리, 가까운 곳부터 차례대로 탐색하는 방식이에요.
특히 거리나 이동 횟수가 중요한 문제에서 자주 사용돼요.

 

BFS의 핵심은 탐색 순서에 있어요.

• 현재 위치에서 가장 가까운 정점부터 차례대로 방문해요.
• 탐색이 자연스럽게 레벨(level) 단위로 진행돼요.

즉, 시작 지점에서 1칸 떨어진 곳들을 먼저 탐색하고, 그다음 2칸, 3칸 떨어진 곳으로 범위를 넓혀 가요.

 

BFS의 동작 방식

이런 탐색 방식 때문에 BFS는 큐(Queue)를 기반으로 동작해요.

• 먼저 발견한 정점을 큐에 넣어요.
• 큐에 먼저 들어온 정점부터 차례대로 꺼내서 처리해요.

이 구조 덕분에 BFS에서는 거리 개념이 자연스럽게 생겨요.
어떤 정점을 처음 방문했을 때의 거리가 곧 시작 지점으로부터의 최단 거리가 돼요.

 

아래는 BFS의 기본적인 초기 설정 코드예요.

queue<int> q;
visited[start] = true;
dist[start] = 0;
q.push(start);

 

BFS에서 중요한 포인트는 두 가지예요.

1. 큐에 넣는 시점에 방문 처리를 해요.
   그래야 같은 정점이 큐에 여러 번 들어가는 걸 막을 수 있어요.
2. 거리 배열(dist)을 함께 관리해요.
   현재 정점의 거리에서 +1 한 값을 다음 정점에 저장해요.

이 방식 덕분에 BFS는 별도의 계산 없이도
각 정점까지의 최단 거리를 구할 수 있어요.

 

BFS의 특징을 정리하면 다음과 같아요.

• 최단 거리를 보장해요.
  간선 가중치가 동일한 그래프에서는 항상 올바른 답을 줘요.
• 메모리 사용량이 DFS보다 큰 경우가 많아요.
  한 레벨의 정점들을 큐에 동시에 저장해야 하기 때문이에요.

DFS vs BFS - 언제 무엇을 써야 할까요?

---

DFS와 BFS는 서로 우열을 가리는 관계가 아니에요.
문제의 조건에 따라 더 잘 맞는 선택이 달라질 뿐이에요.

 

아래는 자주 등장하는 상황을 기준으로 한 정리예요.

상황	추천	이유
모든 경우를 탐색해야 할 때	DFS	구현이 간단하고 백트래킹에 유리해요
최단 거리를 구해야 할 때	BFS	레벨 단위 탐색으로 최단 거리를 보장해요
경로 존재 여부만 확인할 때	둘 다 가능	문제 조건과 구현 난이도에 따라 선택해요
탐색 깊이가 매우 깊을 때	BFS	재귀로 인한 스택 오버플로우를 피할 수 있어요

 

DFS와 BFS 중 항상 정답인 선택은 없어요.
대신, 다음 질문에 답해보면 선택이 훨씬 쉬워져요.

• 이 문제는 모든 경우를 끝까지 봐야 할까요?
• 거리나 이동 횟수가 중요한가요?
• 그래프의 깊이나 크기는 어느 정도인가요?

결국 문제의 조건이 탐색 방법을 결정해요.
이 기준을 머릿속에 두고 문제를 바라보면, DFS와 BFS는 더 이상 헷갈리는 개념이 아니라 도구로 느껴질 거예요.

 

DFS와 BFS의 차이는 구현 방식이 아니라, 탐색 순서를 어떻게 가져가느냐에 대한 전략의 차이예요.
둘 중 무엇이 더 좋은지는 중요하지 않고, 문제에 더 잘 맞는 선택이 무엇인지가 핵심이에요.

 

그래서 문제를 풀기 전에, 먼저 아래 질문부터 던져보는 게 좋아요.

 

이 문제는 최단 거리를 구하고 있는가? (최솟값)
이 문제가 모든 경우의 수를 탐색해야 하는가 (완전 탐색)

 

이 질문에 대한 답이 정해지면, 그다음에 DFS와 BFS 중 어떤 알고리즘을 쓸지도 자연스럽게 결정돼요.

 

알고리즘을 외우는 데서 멈추지 않고, 문제를 해석하는 기준으로 탐색 방법을 선택하는 것이 그래프 탐색을 제대로 이해하는 첫걸음이에요.